Will bonding curves be researchers’ best friends?

Continuous token bonding curves, formerly referred to as curation markets, describe a blockchain framework that is different from the concept underlying the now widely known cryptocurrency Bitcoin.

The first description of curation markets originates from Simon de la Rouviere. Click this link to read his 2017 whitepaper. Zap relabelled curation markets to bonding curves. In de la Rouviere’s words,

A curation market is a smart contract on Ethereum that is deployed for a specific shared goal or topic that allows the minting of tokens set by a hard-coded algorithm.

Being not quite the right kind of geek, I felt that the original publications I had come across were lacking a diagram to aid my understanding. Here is my attempt in putting de la Rouviere’s idea into a visual.

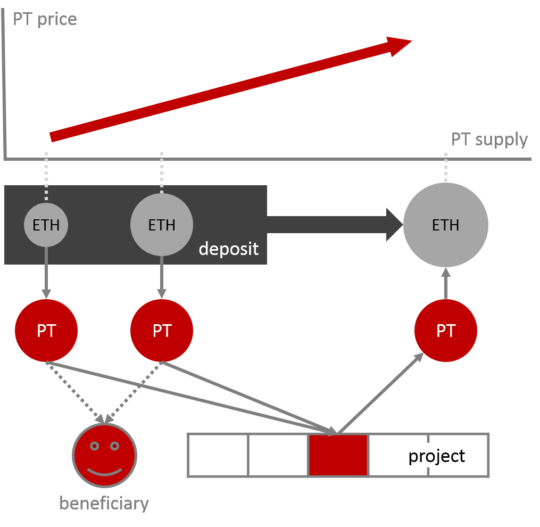
So, what’s the story?

The core idea is that the price of project tokens (PT) changes with their supply in a pre-determined manner. This means the price is always known along the price-supply curve. There is less room for manipulation than with cryptocurrencies like Bitcoin. The curve can be of any shape as prescribed by code. The original proposal included a slow exponential increase. Since the underlying smart contracts are on Ethereum, PT can be bought with Ether (ETH). The amount of PT that can be minted (created) anytime is theoretically only limited by the available ETH in the world. Thus, minting and bonding curves are continuous.

People who obtain PT can bond (assign) these to a project or specific sub-project (red box amongst all project features in diagram). In a way, this can be equated to ‘likes’ or ‘upvotes’ on social media (hence curation market). Investors can either make this decision themselves or use a trusted curator as an intermediary. The latter would be like voting for a politician who you expect to back legislation you care about. The more PT are invested in a sub-project, the more confidence or demand in it exists within the participating community. As more people join the same sub-project, the supply of bonded PT rises and so does the price. This means, more ETH is needed to get the same amount of PT. If an early investor eventually decides to take out (‘burn’) their PT from a successful sub-project, they stand to receive more ETH than they invested. The profit amount depends on the shape of the programmed curves. Buying and selling curves do not have to be identical.

In addition to the project, there can be a hardcoded optional beneficiary who receives a proportion of the invested ETH or PT. Allocating ETH to the beneficiary harbours a greater risk of misalignment of incentives. By allocating PT, their fate is more closely linked to the success of the sub-project. These split funds could, for example, sustain an umbrella organisation that manages projects. Obviously, this reduces the possible gain. From the investor’s perspective, it is like an upfront fee.

The invested ETH are all kept in a communal deposit. Locking ETH up incurs an opportunity cost because it cannot be traded elsewhere. Thus, the decision to invest in bonding curves is influenced by external markets. Because PT price adjusts automatically with supply, there are always enough ETH to pay out all investors according to their place on the bonding curve. This market is always liquid. Secondary markets for PT can also be created.

A bright future for science?

Part of my interest in blockchain and bonding curves stems from personal experiences as an academic biomedical researcher. The journal ranking-driven publication pressure in academia does not only have positive effects on scientific exploration. The often-repeated mantras “publish or perish” and “You’re only as good as your next paper.” say a lot already. But you cannot just publish anywhere. It must be a reputable journal, i.e. the high-ranking ones everybody cites. How do you get in?

Besides the chronic funding problem to finance in-depth quality research, two specific hurdles are editors and peer-reviewers. So, a handful of people decide whether your results are not just interesting and robust but also sufficiently in vogue to be worthy of a decent journal. A well-researched niche topic may not make it because it is assumed that the wider research community does not care enough. It is a bit like clothing fashion. Somebody decides what’s hot this summer. You either ride the wave or remain uncool. This creates a temporary bias in research focus. A related concern is that papers in lower-ranking journals may be undervalued despite good quality work. On the other hand, the pressure to publish often and as high as possible may encourage short-cuts, sloppiness, lack of creativity and, dare I say, fraud. Competing for the spot as first author (especially important for early researchers) can hinder collaboration. Who cares about that little asterisk that points to the small-print statement that the first two names contributed equally? If your last name starts with Z, you have probably lost pole position by default in a joint publication.

A further huge issue is that it is extremely hard to publish negative results. Unless they credibly challenge existing knowledge, you cannot just say, “We’ve tried this, but it didn’t work.” Journals do not care. It does not sell copies because there is no story. Quite likely, many labs repeat the same mistakes independently because they do not know of each other’s failures. Consequently, method optimisation and valuable discovery are delayed.

All in all, there are many problems in current academic science communication and reward systems. Over time, I have become vaguely aware of ideas and projects trying to apply blockchain technology to aspects of science communication (in the widest sense) and intellectual property. There is the promise to ‘fix’ the system by weeding out bad and rewarding good science, enhancing collaboration and making publication fairer. A researcher’s dream!

Finally, this is me getting started in exploring those new shores. With this post I am sharing my understanding of the basics of continuous token bonding curves. Feedback and pointers to further resources are very welcome. This is all part of a learning journey.

Main References

• https://docs.google.com/document/d/1VNkBjjGhcZUV9CyC0ccWYbqeOoVKT2maqX0rK3yXB20/edit (accessed 24 Aug 2019)
• https://medium.com/@simondlr/introducing-curation-markets-trade-popularity-of-memes-information-with-code-70bf6fed9881 (accessed 24 Aug 2019)
• https://medium.com/@simondlr/tokens-2-0-curved-token-bonding-in-curation-markets-1764a2e0bee5 (accessed 24 Aug 2019)
• https://medium.com/@ZapUnofficial/zap-bonding-curves-explained-63e3a92cd009 (accessed 24 Aug 2019)
• https://medium.com/coinmonks/token-bonding-curves-explained-7a9332198e0e  (accessed 24 Aug 2019)